[Recommend my two-volume book for more reading]: BIT & COIN: Merging Digitality and Physicality
The COPA v. Wright trial ended on March 14, 2024. Judge Mellor made an oral statement at the closing of the trial that was quite shocking, especially for people who supported Dr. Wright or were neutral. See Judge’s declaration in COPA v. Wright.
If the written judgment confirms the judge’s declaration that Dr. Wright is not Satoshi, I’ll give due respect to the judgment unless an appellate court overrules it.
As an independent observer, however, I reach a personal conclusion using an objective Bayesian method to estimate the realistic probability based on the evidence that is available to me. To this end, the COPA v. Wright trial has been helpful because it allowed evidence to be more exposed and more thoroughly contested.
My conclusion:
I reevaluated the evidence in light of the trial with calm and respect. At this point, my conclusion is still that Dr. Wright is Satoshi, the inventor of the Bitcoin blockchain.
My conclusion is the result of my objectively applying the Bayesian method to estimate the probability of a hypothesis based on all available evidence.
Regardless, the more significant part of this article is about why the Bayesian method should be used to assess the identity issue, which is probabilistic in nature. This is a critical point that cannot be over-emphasized.
A brief introduction to the Bayesian method
Before we get into specific facts and evidence, I would like to introduce the Bayesian method for estimating the probability of a certain hypothesis. Although the Bayesian method is not the only scientific method for estimating probability, its underlying principle is the only way to correct a common fallacy in people’s estimates of probabilistic matters.
The common fallacy is simply this: we confuse possibility with probability, lock our minds in single factors, and fail to understand the mathematical nature of a probabilistic world that requires sequential progressive iterations of probability estimates based on cumulative evidence.
To a spectator who has no access to the original truth, any outlandish conspiracy theory has a possibility of being true. The human mind leaves a vast room for imagination. It is not a defect in itself. Everyone has a right to speculate, and most of us are probably susceptible to the influence of our interests and likings to various degrees.
But the key is not possibility but probability.
Unless one has direct firsthand access to the original truth, he must focus on finding the objective probability.
If one’s mind pursues only imaginary possibilities but disregards objective probabilities, it either finds no anchor to attach to or, worse, attaches to a false anchor created by personal bias. At that point, the human imagination becomes a problem because the mind is taken over by a ‘mind virus’, which is a carrier of false information.
This mind virus has become a pandemic due to the increasingly available superficial information that floods people’s minds.
This applies to either side of a controversy, so we all need to restrain our minds and hearts with an objective estimate of the probability instead of going loose with unrestrained imagination of a possibility.
An intelligent way to estimate the probability of a hypothesis is to objectively use the Bayesian method of estimating probability, which considers all available evidence together with appropriate weights.
The gist of the Bayesian method is shown in the following figure:
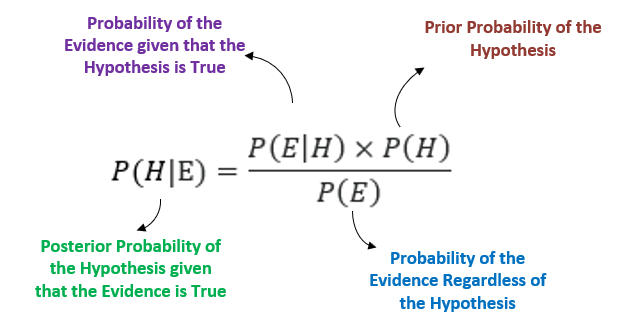
At any given point, you have a temporary probability of a certain hypothesis P(H), which is called prior probability.
With new evidence E, you update the prior probability P(H) to the new probability P(H | E), which is called posterior probability.
Prior probability and posterior probability are relative terms because posterior probability now becomes the new prior probability when new evidence is served for another update iteration, and so on.
For example, say you start with a random person who claims to be Satoshi. Assume that the person has not produced any concrete evidence to support the identity claim, except that he is a real person (who actually lives or has lived) and was in adulthood in the time frame contemporary with Satoshi. With such near nonexistent evidence, P(H) can be assumed to be very low, say 10^-9 (1 billionth).
From there, we then start to use the available evidence, one independent piece at a time, to approach the more accurate estimate of the probability based on evidence P(H | E), which stands for the updated probability of the hypothesis given evidence E.
Back to the Bayesian equation:
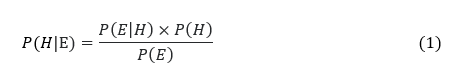
Where
- P(H) is the prior probability of the Hypothesis
- P(H | E) is the posterior probability of the Hypothesis
- P(E | H) is the conditional probability that the Evidence is true if the Hypothesis is true.
- P(E) is the total probability that the Evidence is true whether the Hypothesis is true or not.
Note that, from the above Bayesian equation, P(H | E) is an update of P(H) using a simple multiplication:
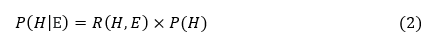
Where

R(H, E) is an update factor, a variable dependent on H and E.
That is, we start with prior probability P(H) and update it to posterior probability P(H | E) by simply multiplying prior probability P(H) with an update factor R(H, E).
Now, all the mathematical action lies in determining the update factor R(H, E) in each update step (called an iteration).
R(H, E) is a ratio between two probabilities P(E | H) and P(E), as shown in the above equation (3).
In the R ratio, the numerator is the probability of the evidence given that the hypothesis is true, while the denominator is the total probability of the evidence regardless of the hypothesis.
The essence of the Bayesian methodology has the following elements:
- In each iteration, realistically figure out the ratio R(H, E).
- Unless the evidence is an absolute logical impossibility or contradiction, never give R(H, E) an extreme value “0” (because doing so makes all other evidence irrelevant), but always give a realistic estimate of the probabilities.
- Never lock your mind into an isolated step by assuming that R is the posterior probability you’re looking for. R(H, E) is a factor used to compute the posterior probability, not the posterior probability itself.
The above (2) and (3) combined are critical because human psychology tends to reach a conclusion based on a single factor. Even if we consciously consider multiple factors, we may still fail to mathematically connect the multiple factors to result in a proper accumulation of evidence.
For example, let’s say you somehow have evidence that the person who claims to be Satoshi committed forgery. For the sake of illustration, let’s say you are highly confident that the person committed forgery (note that this in itself is usually an exaggeration because multiple factors may mitigate or negate that conclusion—for the sake of illustration, however, let’s assume this is justified).
At this point, an irrational person might jump to the conclusion that the claimant is absolutely not Satoshi because a real Satoshi would absolutely not commit a forgery. But that is irrational and is exactly why we need Bayesian methodology.
Using Bayesian methodology, you estimate the update factor R(H, E) based on the evidence. The above is estimated as follows:
- Estimate P(E | H), which is the probability that if the person is indeed Satoshi, he may commit a forgery.
- Estimate P (E), which is the total probability that the person, whether he is Satoshi or not, may commit a forgery.
At this point, you may realize that the update factor R(H, E) has to do with measuring the character of Satoshi against an average person. You’d be right if you do, but there’s more.
Let’s say you believe that the probability of Satoshi committing a forgery is 1/100 (0.01), while the probability of an average person committing a forgery is 1/10 (0.1). This means that you believe Satoshi is 10 times less likely to commit forgery than an average person would. This may be favoritism, but let’s say it is reasonably justified.
You might then conclude, incorrectly, that R(H, E) = 0.01/0.1 = 0.1.
With the above R, which is more reasoned (but still incorrect – see below), you at least have escaped from the pit of jumping to a conclusion predicated on a single factor. But if you’re not using the Bayesian method, you might still jump to the wrong conclusion that there is only a 1/10 chance that this claimant is Satoshi. Although this is a more reasonable conclusion than concluding that there is no possibility that the claimant is Satoshi, you’d still be mathematically wrong.
You’d be wrong because, in the above case, P(E) is not 0.1!
Rather,
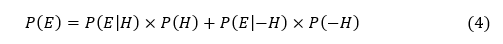
Where
- P(E) = Probability that the Evidence is true whether the Hypothesis is true or not. P(E) is the total Probability of Evidence.
- P(H) = Prior Probability of the Hypothesis being true.
- P(-H) = Prior Probability of the Hypothesis not being true. This is the probability that the Hypothesis is not true based on the prior evidence and independent of the Evidence in the current iteration. Note that the sum of two probabilities P(H) and P(-H) is necessarily 1. That is, P(H) + P(-H) = 1, constituting a complete statistical ensemble.
- P(E|-H) = Probability of the Evidence given that the Hypothesis is not True.
The above Bayesian equation shows the following important truth:
P(E), the total probability of the evidence, is not independent of the prior probability P(H) of the Hypothesis. It depends on it.
This is critical.
For example, let’s start with the above example where a random person claim to be Satoshi and earned a probability of 0.00000001. Not only that,, evidence indicates that he likely has committed forgery.
We have:
P(H) = 0.000000001 (prior probability), and
P (E) = 0.01 x 0.000000001 + 0.1 x 0.999999999 ≈ 0.1
Because P(E | H) = 0.01, we have:
R(H, E) = P(E | H) / P (E) = 0.01/0.1 = 0.1
Therefore, the updated probability(posterior probability) is as follows:
P(H | E) = R(H, E) x P(H) = 0.1 x 0.000000001 =0.0000000001
Therefore, such a person’s already extremely low probability of being Satoshi is further reduced by another factor of 10.
The above result is probably not surprising.
However, let’s examine a different scenario.
Let’s assume that, by using other evidence, we have previously reached a Bayesian probability of 0.999 that the person is Satoshi. That is:
P(H) = 0.999
Now, with the new evidence that the person may have committed forgery, we would have:
P (E) = 0.01 x 0.999 + 0.1 x 0.001 = 0.01009
Because P(E | H) = 0.01, we have:
R(H, E) = P(E | H) / P (E) = 0.01/0.01009 = 0.99108
Therefore, the updated probability(posterior probability) is as follows:
P(H | E) = R(H, E) x P(H) = 0.99108 x 0.999 ≈ 0.99
That is, even with the devastating evidence that the claimant has committed forgery, and further, even with a favoritism assumption that Satoshi is 10 times more moral than an average person, the probability that the claimant is Satoshi is still at least 0.99, practically near certainty.
How is the above second scenario different from the first one? It is because R(H, E) depends on posterior probability P(H). In the above second scenario, the other evidence has brought the prior probability to 0.999. The unfavorable new evidence updates it to posterior probability by reducing it to 0.99. The posterior probability is reduced but still very high.
Important Bayesian lessons
The Bayesian probability estimate often strikes people as counterintuitive, but this is only because we fail to realize the interdependence of various probabilities.
1. Injecting certainty to a probabilistic matter is a fatal logical fallacy
In the above example, the simplistic logic that ignores the Bayesian reality goes like this: Because the real Satoshi will not forge a document to support his claim, and therefore one who has forged a document cannot be Satoshi. This may sound like simple logic, but one who thinks that way is trapped in presumptive certainties, thus failing to objectively and scientifically estimate the probabilities.
Here is why: The above fallacious logic falsely injects certainties into probabilistic matters. The statements “Satoshi will not forge a document” and “the claimant has forged a document” are probabilistic matters. But the false logic falsely presumes certainties of these matters. These certainties are simply presumed, not questioned or tested scientifically nor estimated mathematically, but just felt, often with passion.
If you assume that Satoshi would absolutely not produce a forged document under any circumstance, you would have P(E | H) = 0. As a result, the Bayesian equation would always result in R(H, E) = 0, and consequently, the posterior probability would be fixed at zero because P(H | E) = 0. This renders the other factors irrelevant in the Bayesian iteration.
But the question is, how can you be so sure that the possibility of Satoshi forging a document is absolutely zero? Simply making that assumption is committing a logic error.
What makes the above logic error even more egregious is that it erroneously assumes absolute determination that the document is indeed intentionally forged with a specific intent of fraud. This itself is a probabilistic matter that deserves a separate Bayesian inquiry. Even if we don’t get into a secondary Bayesian inquiry, on its face, the above logic error is worse than merely saying that “Satoshi would never forge a document”, but is rather equal to asserting the following:
“If the person were Satoshi, he would have never provided a document that has questionable authenticity” (or “if the person were Satoshi, such a scenario of presenting documents of questionable authenticity could absolutely not have happened in any circumstance”).
Note that the above is an even more erroneous assumption. The reality in COPA v. Wright was that some documents’ authenticity was questionable but not proven to be forged. Further, even if the documents had a high probability of being forged, they’d invoke a series of additional probabilistic inquiries. “Was it intentionally forged by Dr. Wright and submitted as evidence?” “Was it unintentionally created by some other processes?” Or “Was it created by some other persons with a different motive?” And so on.
The probabilistic nature of these inquiries means that one cannot inject certainty into the inquiry of whether Dr. Wright has committed a fraudulent forgery in the first place. Furthermore, even with a highly probable finding of fraudulent forgery, it does not make the identity question determinative. It is a probabilistic matter and needs to be scientifically determined using the Bayesian method (see above).
Given the probabilistic nature of these matters, one simply cannot assume P(E | H) = 0. Doing that destroys all the probabilistic reality.
Yet that is precisely what people tend to do. The trial of COPA v. Wright is an epic demonstration of how lawyers and judges do exactly that.
2. Probabilities are dynamically linked in reality, not isolated
Further, in reality, these probabilities interact with each other in the Bayesian equations.
For example, if the prior evidence has already resulted in the high P(H), which is the prior probability of the person being Satoshi, then the assumption (or knowledge) that the real Satoshi has a low probability of forging a document would also mean that a person in question has a low probability of forging a document when he has a high probability to be Satoshi.
This is not a circular logic. It just means that the two probabilities are dynamically linked. It is a fundamental probabilistic nature of the real world in which we exist.
As a result, if you start with a presumptive certainty that the person has definitely forged a document without allowing any room for a probabilistic adjustment based on related evidence, you have effectively destroyed this dynamic link and thus distorted the reality of Bayesian probability.
Likewise, if you try to determine the target posterior probability P(H | E) without any regard to the prior probability P(H), you also break the links between these various probabilistic conditions.
When you do any of the above, you are no longer scientifically estimating reality but only manipulating an imaginary one, detached from reality, which is linked, both mathematically and physically.
The above is reflected in the Bayesian equation introduced above:
P(E) = P(H) x P(E | H) + P(-H) x P(E |-H),
in which a high P(H) and correspondingly a low P(-H) shift P(E) toward P(E | H) and away from P(E |-H). That is, P(E) ≈ P(H) x P(E | H). Conversely, a high P(-H) and correspondingly a low P(H) shift P(E) toward P(E | -H) and away from P(E | H). That is, P(E) ≈ P(-H) x P(E | -H).
We tend to intuitively think that P(E) is just P(E |-H). But in reality, P(E) is the total probability of the evidence, which is the sum of two components, like a superposition of two alternative states. A high P(H) means a low P(-H), and vice versa because P(H) + P(-H) = 1.
In the above example, for instance, we happen to have a high prior probability P(H), and correspondingly a low P(-H). These probabilities together bring P(E) close to P(E | H), which is 0.01, instead of P(E |-H), which is 0.1. This makes the Bayesian update factor R(H, E) closer to 1 (0.01/0.01009 = 0.99108) rather than to 0.1 (0.01/0.1 = 0.1), leading to a very different P(E) than what one tends to assume reflectively. It is different, namely 0.01 vs. 0.1, but is the correct result.
The above error is not merely theoretical, but something that we unconsciously commit all the time.
If you bring a Bayesian view to the trial of COPA v. Wright, you will see that COPA tried all it could to ignore the prior probability P(H) that should be derived from other evidence, and focused on forgery allegations as if those were isolated and independent probabilistic events when they were not. It was essentially an attempt to lead people to subconsciously mistake a fixed probability derived from a certain piece of evidence for the target probability, which should be a cumulative result of linking all available evidence.
In addition to the forgery allegations, here is another example: During his cross-examination that lasted for weeks, Dr. Wright had one (and only one) occasion in which he seemed to stumble. He couldn’t give a quick and straight answer to the question of what a signed integer is. Unsurprisingly, this incident caused people to say on social media that Wright could not possibly be Satoshi because it is impossible that Satoshi would not know the answer to such a basic question. But again, this is an irrational and unscientific reaction that assumes false certainties. But in reality, is a very typical probabilistic iteration of evidence (or an event) for Bayesian probabilities.
First, his answer was correct, even though it did not come out smoothly. If this point is debatable, it is a technical matter. If an accurate technical determination were made during the trial, it would not be a probabilistic matter. But because no determination was made, that issue itself becomes a probabilistic matter, subject to Bayesian estimation.
Second, a person’s knowing an answer is very different from his being able to immediately come up with a smooth articulation during a long, stressful, and exhausting cross-examination. Although Satoshi would almost certainly know the answer, that alone is not determinative. What is the most relevant in this part of the Bayesian estimation is not whether Satoshi knows the answer or not, but a comparison between the following two probabilities:
- P(E | H) – the probability that Satoshi would stumble on a rare occasion in articulating something that he knows given the specific circumstance (a lengthy trial cross-examination, a carefully devised attack question, etc.) and
- P(E |-H) – the probability that a person other than Satoshi would do the same.
And further, one needs to calculate the update factor R (H, E) using the above Bayesian equation (2).
If you do an honest Bayesian exercise based on objective assumptions, you will find that the above episode is essentially a nonevent, because it does not significantly affect the posterior probability, unless you deliberately idolize Satoshi into someone who never gets tired, never slips on memory, and never stumbles in articulations, and you also refuse to acknowledge that Satoshi could suffer an unusual neurodevelopmental condition such as Asperger’s syndrome that makes him think too hard on simple things.
Judging from the reactions in the courtroom and the social media, people illogically assumed that P(E | H) = 0 and P(E |-H) ≈ 1. But in reality, there is no reason to assume P(E | H) and P(E |-H) are significantly different, because it is not a test of specific knowledge, but a personal behavior. In fact, if anything, P(E | H) may be greater than P(E |-H) if there is evidence that Satoshi suffers Asperger’s syndrome which makes him think too hard about simple things.
Again, the point is this: it is illogical and unscientific to use irrationally assumed certainties to distort Bayesian probabilities, which are the normal reality of the world we live in.
The above illustrates that our subjective feelings about probability can be easily wrong. We must use the scientific method for estimating probability. The Bayesian method is proven to be more scientific and more accurate than people’s reflective reactions to evidence.
A point with repeating is that one must realize that each R (H, E) based on a piece of evidence depends on the prior probability P(H) and is further not the probability of the hypothesis. It is just one of the many update factors in the Bayesian iterations to compute the posterior probability, and it must be computed scientifically at each iteration.
For interested readers, my book BIT & COIN: Merging Digitality and Physicality—Vol. II has a chapter that provides a more complete description and application of the Bayesian method in Satoshi’s identity.
What the COPA trial didn’t change
An important outcome of the trial lies not in what loudly happened but in what is silently implied by that which didn’t happen:
The major factors that contribute as separate and independent iterations of the posterior probabilities of Bayesian estimates were silently confirmed.
These include:
- Testimonies under oath by firsthand eyewitnesses
- Unique background and qualifications
- Personal knowledge with respect to the deep inner workings of Bitcoin and interactions with early Bitcoin developers
- The absence of an alternative Satoshi identity to challenge Dr. Wright’s claim
- Dr. Wright’s apparent reliance on the absence of an alternative Satoshi, as evidenced by his committing tens of millions of dollars, at least a decade of his entire life and his reputation to sustain the claim
- Dr. Wright’s view of Bitcoin matches that of Satoshi far better than anyone in the opposing camp.
These factors, along with many others, together reach an extremely high Bayesian posterior probability of Wright being Satoshi (See Mathematical proof that Dr. Craig S. Wright is Satoshi Nakamoto). The trial did not change them, but only confirmed them, albeit implicitly.
The significance of these confirmed factors is so high that, in view of the Bayesian methodology, allocating overwhelmingly large proportions of the trial time to other issues effectively worked as a distraction because the outcomes of those issues, one way or another, do not change the posterior probability from one direction to another. But again, it was COPA’s strategy, and it worked.
Concerning Dr. Wright’s unique background and qualifications, no serious evidence was produced to dispute the facts. COPA called the world’s most prestigiously certified cyber security expert and the number one prolific inventor in the blockchain and DLT tech fields (both are demonstrable facts) as “just an IT guy” without providing any evidence. I hate to say this, but it was a ridiculous trial act. It indicated either ignorance or prejudice.
The firsthand eyewitnesses were all cross-examined, as expected. But other than simply implying or asserting that the witnesses lied, COPA presented no specific evidence to impeach any of the witnesses. This is not to say that one should accept the testimonies of the eyewitnesses as undisputed truth. It just means that one should fairly give proper probabilities to these sworn witnesses. One should not simply swipe away the credibility of a firsthand witness who testified under oath just because what they testified is something that you are unwilling to believe.
As to the personal knowledge with respect to the deep inner workings of Bitcoin, the knowledge that Dr. Wright has demonstrated went way beyond what the judge and the lawyers could independently interpret and decide. Unfortunately, no expert witness was called to provide support to either side. As an independent observer, I saw what I saw, and I’m confident in making estimates in that regard. See, for example, Is Bitcoin’s Merkle tree a binary search tree? If anything, the trial made this already extremely favorable element even more favorable to Dr. Wright. It’s just that this part of the evidentiary input may have escaped most people, as it has always been.
Overall, it’s hard to tell how much the judge grasped and weighed these facts. In the trial, an overwhelming amount of time was devoted to document authentication, leaving all other foundational questions unexamined and ignored. Again, it was COPA’s strategy, and it has worked.
Where the COPA trial did have an impact
At the same time, the past incidences of private signatures conducted by Dr. Wright were substantially contested during the trial, unsurprisingly. However, everything COPA alleged was based on theoretical possibilities, with zero evidence of how it actually happened. There should be proper legal admonition that no fraud should be alleged without specific evidence. But even if such allegations were considered legitimate on their face, they’re just a matter of probability, which vastly favors Dr. Wright. It is a simple fact that, although it is theoretically possible for someone to fake a private signature, the probability for such a fraud to be successfully committed against someone no less than Gavin Andresen, who is not only technically competent but also possesses unique personal knowledge of Satoshi, is far smaller than that of the opposite.
Again, it is a matter of objective Bayesian probability, not a sentimental yes-or-no binary choice. Prior to the trial, I had already taken the probability of faking such a private signature session into Bayesian estimates. Because the trial revealed absolutely no new information, it didn’t change the Bayesian probability estimate.
On the other hand, the biggest part of the trial that went against Dr. Wright was that he failed to provide further documented evidence that could be of any significant extra value. Many had expected at least some. To the contrary, the additional documents provided a rich attack vector for COPA in their forgery allegations to reduce his credibility.
However, even under the worst assumption against Wright, forgery evidence does not work as an absolute negator in Bayesian iterations because such evidence does not constitute logical falsifications based on impossibility or contradiction. Forgery is a character contradiction rather than a logical contradiction. See The key in COPA v. Wright and To prove a negative in COPA v. Wright.
Forgery evidence should be properly taken into account in Bayesian iterations.
First, the forgery allegations against Dr. Wright were not undisputed. Dr. Wright provided detailed technical explanations to explain why those discrepancies or the appearance of forgeries were a result of certain conditions, including an enterprise working environment that allowed multiple user accesses and automated file synchronizing, and also that he was a victim of internal sabotages.
Unfortunately, no evidence was further provided to support what Dr. Wright said. In the eyes of the judge, without further facts or expert witness support, Dr. Wright’s own testimony cannot be taken as equal, let alone superior, evidence to that of an expert witness. It does not matter how Dr. Wright is technically more competent than the COPA’s expert witness. The judge does not have any basis to evaluate that and may automatically fall back to the expert witness testimonies. If he did, he was just following evidentiary rules.
The Bayesian view of an independent observer
However, as an independent observer outside of court, I (and you should, too) compute the posterior probabilities based on what is presented, not on what the judge has done due to legal procedural restrictions.
Further, even assuming the worst against Dr Wright, that is, assuming that Dr. Wright has committed forgery, the finding is just a separate Bayesian factor that should be taken into consideration in the Bayesian iterations of posterior probabilities. See the previous section, “Brief introduction to the Bayesian method”.
Bayesian posterior probabilities involve a series of multiplications of probabilities, in which a finding of forgery may insert a low number (that is, the probability that the real Satoshi would commit forgery is low, say only 1%, etc.), but it does not constitute a logical impossibility which would insert a zero into the multiplication and renders everything else irrelevant. A low number resulting from a particular piece of evidence (such as forgery) will negatively affect the posterior probability but is not determinative. It is just one piece of evidence among many pieces of evidence, each affecting posterior probability. Its effect can be balanced and outweighed by other countering factors to still result in a very high positive probability in the final result. (See the previous section, “Brief introduction to the Bayesian method” and Mathematical proof that Dr. Craig S. Wright is Satoshi Nakamoto.)
I put everything I’ve seen together and considered them in an objective Bayesian estimate, and my conclusion is still that Dr Wright is extremely likely to be Satoshi.
It doesn’t mean that I have 100% certainty. For complex matters, we never do. It means that I act according to the practical probability as a result of objectively applying the Bayesian method.
With a very high Bayesian probability, I can’t pretend ambivalence. If the probability is between 30% and 70%, or even 20% and 80%, there can be an honest justification for ambivalence and inaction. But if the probability reaches beyond 90% or diminishes below 10%, pretending ambivalence becomes evidently dishonest.
In the case of Dr. Wright’s Satoshi identity, my objective estimate using the Bayesian method gives me a result that is better than 99% that Dr. Wright is Satoshi, even after this trial. This probability is at a point where, barring a clear, logical falsification proof (i.e., a proof of logical impossibility or contradiction, such as a clearly better proof of an alternative Satoshi), I would simply be dishonest if I denied Dr. Wright’s Satoshi identity.
The technology matters more.
Even more importantly, I did not get myself into this because of my curiosity about Satoshi’s mysterious identity. I got into Bitcoin and blockchain because of my conviction of the danger humanity faces and what solutions are helpful (or unhelpful or even harmful).
Regardless of the final outcome of the Satoshi identity case, it is more critical than ever to focus on developing the right technology to solve humanity’s most existential challenge. See TimeChain that preserves humanity in digital age.
I have always focused on technology rather than identity, and I will be even more so in the future. However, when asked who Satoshi is, I will still say Dr. Craig S. Wright. This is not a contempt for the court or the judge, nor a spite toward those who have different views, but only my honesty.
[Recommend my two-volume book for more reading]: BIT & COIN: Merging Digitality and Physicality
Comments are closed