[Recommend my two-volume book for more reading]:
BIT & COIN: Merging Digitality and Physicality
Is Bitcoin’s Merkle tree a binary search tree?
Dr. Wright says Bitcoin’s Merkle tree is a binary search tree (BST). BTC devs disagree and question his qualifications. The questioning by BTC and Dr. Wright’s answers show a typical example of Dr. Wright talking about it at a level and depth that others haven’t thought of.
Ironically, some even question Dr. Wright’s understanding of technology at the undergraduate level, not in spite of this but because of this.
(This same kind of ongoing questioning during the last eight years dominated the Wright Satoshi subject. Frankly, it is shameful and unjust. It is also what often compels me to explain it to others.)
Anyone who might have had the impression that Dr. Wright doesn’t know the basics should reexamine their mindset.
No one should trust what another person says blindly, but a much more common mistake people make about Dr. Wright is rejecting him presumptively. It’s time to learn from what has happened again and again. Judging from past repetitive experiences, the basic sense of prudence would require one to think more deliberately and deeply about what Dr. Wright says, just to avoid embarrassment.
If you truly wish to investigate the truth about Bitcoin, resist the temptation to focus too much on insulated technicalities. It is a system—a system that exists in a computational, economic, and legal environment, to be more particular.
Your understanding of these matters highly depends on whether you want a techno-political system that is primarily for censorship resistance or an economic system that is primarily for productivity. Each view can have its rationales that might be respectful, but one must understand the difference before concluding that others don’t know a thing.
I understand both views very well. I just happen to prefer a scalable and productive economic system to a techno-political law-resistance system. The real world may have room for both systems to exist. My preference has to do with the values I believe in, and I understand others have their own values and beliefs.
So please hear me out on this particular question of Bitcoin’s binary search tree. I discuss it not only because it is of unique technical significance but also because it’s a good example to show why one should pay attention to what Dr. Wright says.
Merkle tree and binary tree
Dr. Wright said the Merkle tree structure that was designed by Satoshi originally and has now been implemented in BSV along with SPV (Simplified Payment Verification) is a binary search tree.
His opponents suggest that it is ridiculously wrong because everyone who has a basic understanding of computer science would know that a Merkle tree is not a binary search tree.
His opponents are right that the conventional Merkle tree, as taught in school, is not a binary search tree in its base form and application.
But what they do not know is that Satoshi had designed the Bitcoin Merkle tree in such a creative way that, although it is a Merkle tree, it is also a search tree, even a binary search tree.
Dr. Wright is just right, once again.
If you come in with a bias against him, you might find that unbelievable. But if you study history, you will find yourself being surprised again and again. It’s a pattern. Perhaps one day you will think to yourself, “Wait, maybe he is…!?”
A more detailed technical explanation
Let me explain the technical details below.
First of all, the key concept about a ‘binary tree’ refers to a feature that cuts the tree (together a corpus of data) in two halves (hence ‘binary’) in every step. It determines the direction to proceed for the next step based on a match or mismatch and discards the half in the other direction. This is repeated until the target item is located. This binary fashion makes the process very fast and scalable. Because every step is a binary, it progresses exponentially, resulting in a logarithmic scalability.
This remarkable effect is created by the fact that half of the data can be instantly disregarded with no risk of losing the target. However, this necessarily requires that the nodes and leaves in the tree are ordered and balanced in a particular way.
Therefore, calling a tree “binary” means that the tree is constructed so that an act (e.g., a search) can be performed in a binary fashion. If the structure does not have this binary feature, then calling it binary would be incorrect. But if the structure does have this binary feature, but no one else knows such a structure and has never called it binary, the one who first calls it would be not only correct but also innovative.
The binary tree can be structured to perform various functions and achieve various goals. When the tree is structured to perform a binary search, it is a binary search tree. However, binary trees can also be used for other purposes, such as ensuring data integrity.
So the question is, why does Dr. Wright call Bitcoin’s Merkle tree a binary search tree?
First, if Bitcoin’s Merkle tree is structured to find the location of a certain piece of data and confirm its existence, it is a search tree. This is plain, regardless of what others say.
But is it ‘binary’ and hence a binary search tree? That is a more elaborate consideration.
The answer is yes. Bitcoin’s Merkle tree is a binary search tree because the Bitcoin data is deliberately structured as a key-value database, meaning that each item (a transaction or a hash) is associated with (labeled by) a key. The keys are sequential. There are different ways to structure the keys. It depends on the design of the tree structure and the algorithm (see below for an example). Note, here, the word “key” is a standard database terminology, like a label of an item, and has nothing to do with cryptography keys.
Because Bitcoin transactions are timestamped according to the order of time each transaction is received, this sequential order is natural. Now, with the sequential keys built in, each corresponding to a timestamped sequential transaction, you have an ordered and balanced tree of hashes of leaves.
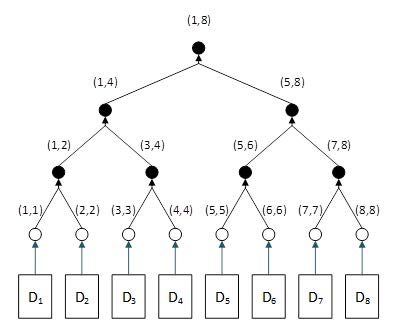
Figure 1 shows an example of such a Merkle tree that is also a binary search tree.
Di denotes transactions. Transaction Di corresponds to hash (i, i), which is a special case of key (i, j) where i=j.
Each node is denoted by a key consisting of a pair of numbers (i, j), such as (1, 4). The meaning of the numbers is quite simple: a node with a key (i, j) means that the data in the node and the child nodes under it cover transactions in the range of i to j. For example, (1, 4) means that the node and the child nodes under it cover transactions 1, 2, 3, and 4. Implicitly, it also means that they are unrelated to transactions 5, 6, 7, and 8, which are covered by the other branch under (5,8).
According to this sequential numbering, (i, k) and (k+1, j) are two neighboring nodes, as indicated by k and k+1. When two neighboring hashes H(i, k) and H(k+1, j) are concatenated and hashed, it generates a new hash H (i, j). The resulting keys (i, j) are logical because concatenating two neighbor hashes concatenates the two ranges, namely i to k and k+1 to j, to create a new range i to j. Hence, its resulting hash is denoted as H (i, j). Note that the middle numbers k and k+1 do not appear in the new key (i, j). This is because the range i to j denotes an extended range that necessarily covers the middle numbers k and k+1.
Figure 1 illustrates a simple case where i=1, 2,…8. In reality, i=1, 2,…n, where n is the total number of transactions in the block and can be a large number.
Merkle tree is formed as follows:
- Hash each transaction Di to get H(i, i). This is the first level of the Merkle tree, in which transaction data items and their hashes have a 1-to-1 correspondence.
- Hash the concatenation of every pair of neighboring H(i, i) and H(i+1, i+1) to get H(i, i+1). This gets the second level, which will have n/2 nodes.
- Repeat the same process in step 2 above until we reach the final level where only one node remains. This is the Merkle root.
Because the number of nodes in each next level is halved, this process reaches the root (top) quickly. The total number of levels m=log2(n). The more transactions the block has, the greater advantage it enjoys.
For example, when n = 8, m = 3. When n = 1 million, m = 20; when n = 1 billion, m = 30; when n = 1 trillion, m = 40, and so on. You can see that, from n=8 to n=1 billion, the total number of transactions in a block has increased more than 100 million times, while the total number of levels in the tree has increased only 10 times.
The above is the basic characteristics of the Merkle tree.
But it will be clear that labeling the nodes using sequential keys transforms the Merkle tree into a binary search tree.
In the example shown in Figure 1, suppose we need to search for transaction D5. which corresponds to key (5, 5). We start from the top (root) H(1, 8), which indicates that the block has a total of 8 transactions from 1 to 8).
First, we compare our target (5, 5) with the present node (1,8). Because 5 > 8/2, we know our target is on the right side. We go to the right side to arrive at node H(5, 8) and disregard the entire left branch, which is half of the tree. If this is not obvious in this small example, imagine that if the block has 1 billion transactions, this one step skips 500 million transactions.
Next, we compare our target (5, 5) with the present node (5, 8). Because 5=5, we know we already got this part of the key correct, which is the lower boundary of the transaction range. But because 5<8, we go to the left and reach H(5,5), which corresponds to transaction D5, the exact transaction we are looking for.
Thus, the Merkle tree shown above enables binary search and is thus a binary search tree. This cannot be debated because it is precisely how a binary search tree is defined.
Such a binary search tree combined with an elaborate design of SPV makes Bitcoin as implemented in BSV extremely powerful.
Binary search tree (BST) and SPV
SPV itself is another subject matter. Although it has been disclosed in the Bitcoin white paper, SPV has only been properly understood and further developed on Bitcoin SV (BSV). I will skip an explanation of SPV itself, but would like to emphasize it’s relevant to Bitcoin’s binary search tree.
SPV is about scalability. If you only look at an individual incidence of how SPV works with a user submission of the Merkle path of his transaction, it would seem that it has nothing to do with search because the user readily produces the Merkle path, which specifically locates not only the transaction ID but also its location, leaving nothing else to be searched on the blockchain. The only thing that remains is that the recipient needs to compute a Merkle proof to verify the existence of the transaction using the Merkle path.
But remember, SPV is about scalability. It means that it’ll work on a blockchain that has billions or even trillions of transactions in a single block. On such a scaled blockchain, scalable and efficient search becomes absolutely essential, for otherwise, everyone, including the sender, the recipient, and the service providers, will be at a loss.
So a scalable blockchain needs scalable search along with SPV. But what else can do scalable search better than a BST?
BST and SPV thus work together like a hand-in-glove. That is what BSV has done. The upcoming Teranode under testing is going to showcase these features. If you don’t care about a scalable system, you may not be excited to hear this. But that doesn’t mean you should puff up to declare that Dr. Wright is ignorant because he says things like the Bitcoin Merkle tree is a BST. Rather, you should realize your own ignorance and failure to understand what he says.
Binary search tree (BST) and text search
Note that we are talking about the structural aspect of BST here, not text search for actual data. Searching for actual data requires lookups. This is commonly done using Trie, a tree-like structure specifically designed for efficient text-based searches, or hash tables that allow access to data using mapping of a text with its hash. But that is irrelevant to the subject matter discussed here.
BST searches the keys associated with the nodes and then uses the keys to identify and position the nodes. This is different from searching for the actual content of data in the nodes, such as full-text search. That is a given. But that does not mean BST is useless just because it does not search the text of data or transactions.
BST primarily serves as a means of organizing the tree, maintaining its sorted order, and informing the system and users of the state.
The truth is that the kind of BST search described in this article works with SPV to enable massive scaling.
Both BST and SPV were in Satoshi’s original design, except that the whitepaper does not mention BST at all and only mentions SPV’s general frame of design.
Those who deny the above truth must start with an unreasoned presumption that Dr. Wright is not Satoshi even to persuade themselves.
This article just shows the consistency in Dr. Wright’s claim and a logical error in his opponents’ claim of the opposite. It might be a stretch to use BST and SPV as evidence to support Dr. Wright’s Satoshi claim, but that’s not what I do in this article.
The point is that Dr. Wright is right in saying Bitcoin’s Merkle tree is also a BST. In contrast, it is outright erroneous to assert that he is ignorant of Bitcoin’s design (and therefore could not be Satoshi) because he says Bitcoin’s Merkle tree is also a BST. The opposite is true. Those who make the assertion are ignorant of Satoshi’s intricate design of Bitcoin.
[Recommend my two-volume book for more reading]: